
Halo sobat Exsight! Tahukah kalian terdapat salah satu metode statistik yang sangat erat kaitannya dengan dunia medis bernama analisis survival. Sesuai dengan namanya “survival” atau ketahanan hidup, analisis survival berkaitan dengan waktu yang dicapai suatu objek hingga terjadi suatu event tertentu. Event dalam hal ini dapat berupa kejadian yang positif maupun negatif.
- Event Positif : Kesembuhan
- Event Negatif : Mulai terjangkit suatu penyakit, penyakit kambuh, kematian
Analisis Survival
Elemen Analisis Survival
Perlu diperhatikan bahwa pada dalam analisis survival terdapat 2 elemen utama yang tidak boleh terlewatkan yaitu Waktu Survival (T) dan Status Tersensor (d). Apa sih itu?
- Waktu Survival = Waktu yang menunjukkan lama seseorang dapat survive selama periode pengamatan tertentu
- Status Tersensor = Status yang menandakan seseorang survive atau tidak. Simbol yang digunakan apabila seseorang sedang mengalami event (d=1) dan sebaliknya ketika tidak sedang mengalami event (tersensor) disimbolkan dengan (d=0).
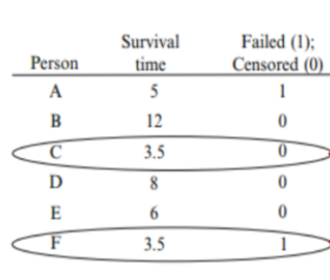
Berdasarkan Gambar 1. di atas terlihat bahwa terdapat 6 pasien yaitu A, B, C, D, E, dan F. Misalnya event yang digunakan yaitu “terjangkit penyakit leukimia”. Apabila kita perhatikan untuk pasien C memiliki survival time 3,5 (bisa dalam satuan jam, hari, bulan menyesuaikan peneliti) dimana pasien C memiliki keterangan status tersensor 0, artinya pasien C tidak mengalami event atau tidak terjangkit penyakit leukimia.
Sedangkan untuk pasien F dengan survival time 3,5 memiliki status tersensor 1 artinya pasien F terjangkit leukimia.
Suatu kondisi ketika seseorang (individu) tidak mengalami event atau tersensor dapat disebabkan oleh beberapa faktor, yaitu:
- Termination of study : Penelitian telah berakhir, namun individu yang diamati tidak mengalami event.
- Lost of following up: Individu menghilang dari pengamatan, padahal penelitian masih berlangsung.
- Withdraws from study : Selama penelitian terdapat individu yang meninggal dikarenakan oleh sebab lain.
3 Tujuan Utama Analisis Survival
- Mendapatkan Estimasi & interpretasi fungsi Survival dan fungsi Hazard dari data survival
- Membandingkan fungsi Survival dan fungsi Hazard
- Mengetahui pengaruh dari variabel prediktor terhadap waktu survival
Fungsi Survival dan Fungsi Hazard
Terdapat dua istilah kuantitatif yang umum terdapat pada analisis survival yaitu Fungsi Survival dan Fungsi Hazard.
Fungsi Survival adalah suatu fungsi yang digunakan untuk menggambarkan fenomena peluang suatu individu dapat bertahan hidup lebih dari waktu t. Fungsi Survival disimbolkan dengan S(t). Adapun rumus umum untuk fungsi survival adalah sebagai berikut.

Fungsi Hazard adalah suatu fungsi untuk mendefinisikan kelajuan individu ketika mengalami event pada interval waktu t sampai (𝑡 + ∆𝑡) jika individu tersebut diketahui belum mengalami event sampai dengan waktu t. Fungsi Hazard disimbolkan dengan h(t). Rumus umum untuk Fungsi Hazard adalah sebagai berikut.

Fungsi Survival dan Fungsi Hazard saling berhubungan, dimana hubungan antara keduanya dirumuskan sebagai berikut.

Kurva Survival Kaplan Meier dan Uji Log-Rank
Analisis survival erat kaitannya dengan adanya Kurva Survival Kaplan-Meier beserta Uji Log Rank.
Kurva Survival Kaplan-Meier memperlihatkan hubungan antara estimasi fungsi survival pada waktu (t) dengan waktu survival nya yang digambarkan berupa suatu kurva. Persamaan umum Kurva Survival Kaplan-Meier dapat dirumuskan sebagai berikut.

Selanjutnya untuk melihat adanya perbedaan Kurva Survival Kaplan-Meier diantara kelompok yang berbeda, maka dapat dilakukan pengujian menggunakan Uji Log-Rank. Hipotesis yang digunakan untuk Uji Log-Rank adalah sebagai berikut.
H0 : Tidak terdapat perbedaan pada kurva survival antara kelompok yang berbeda
H1 : Minimal terdapat perbedaan pada kurva survival antara kelompok yang berbeda.
Adapun statistik uji pada Uji Log-Rank adalah sebagai berikut.

Apabila berdasarkan perhitungan statistik uji Log-Rank, hasil yang didapatkan yaitu:

Maka kesimpulan yang didapatkan yaitu Tolak H0, artinya minimal terdapat perbedaan pada kurva survival antara kelompok yang berbeda.
Model Cox Proportional Hazard
Model Cox Proportional Hazard adalah suatu metode semiparametrik (perpaduan metode parametrik & non parametrik) untuk memodelkan hubungan antara variabel prediktor (satu atau lebih) dengan variabel respon berupa waktu survival.

Berdasarkan model Cox Proportional Hazard, selanjutnya melakukan estimasi parameter menggunakan metode Maksimum Partial Likelihood Estimation (MPLE). Perhitungan dengan metode MPLE dilakukan dengan cara memaksimumkan fungsi partial likelihood. Adapun fungsi partial likelihood dari model Cox Proportional Hazard adalah sebagai berikut.

Tahapan berikutnya yaitu memaksimumkan turunan pertama fungsi ln L(β) dan disamadengankan 0. Kemudian dikarenakan hasil estimasi parameter yang diperoleh bersifat implisit, maka dari itu digunakan metode itersi numerik, yaitu metode Newton Rhapson.
Hazard Ratio
Hazard Ratio (HR) merupakan indikator untuk melihat perbandingan tingkat resiko antara individu dengan kondisi variabel prediktor X dengan kategori sukses serta individu dengan kategori gagal. Sukses dalam hal ini maksudnya individu mengalami event atau status tersensornya (d=1) sendangkan gagal dimaksudkan untuk individu yang tidak mengalami event atau status tersensirnya (d=0).
Nilai estimasi dari Hazard Ratio diperoleh dari hasil perhitungan eksponensial dari masing-masing koefisien dari variabel prediktor di Cox Proportional Hazard yang memiliki nilai signifikan dengan nilai hazard rate. Adapun rumus yang digunakan untuk menghitung hazard ratio adalah sebagai berikut.

Makna dari nilai hazard ratio yaitu menyatakan tingkat kecepatan terjadinya event (laju kegagalan) untuk individu dengan kategori tersensor (d=0) sebesar eβ kali dari tingkat kecepatan terjadinya resiko peristiwa event (laju kegagalan) pada individu dengan kategori tersensor (d=1).
Asumsi Proportional Hazard (PH)
Asumsi Proportional Hazard (PH) merupakan suatu asumsi dimana merupakan Hazard Ratio (HR) yang menyatakan risiko proporsional individu terhadap individu lainnya, dimana bersifat konstan terhadap waktu. Terdapat 3 pendekatan untuk menguji apakah suatu data survival memenuhi asumsi Proportional Hazard yaitu sebagai berikut.
- Pendekatan Grafik
Pendekatan grafik pada asumsi proportional hazard dilihat berdasarkan pola dari plot ln [ -ln (S(t))] terhadap waktu survival (t) untuk setiap variabel prediktor dengan skala kategorik dan grafik observed versus expected kurva survival.
Grafik dikatakan baik atau memenuhi asumsi proportional hazard apabila plot antar kategori dalam variabel prediktor membentuk pola yang sejajar serta berhimpitan pada grafik observed versus expected kurva survival.
- Pendekatan Goodness of Fit
Pendekatan goodness of fit pada asumsi proportional hazard dilihat berdasarkan nilai dari residual Schoenfeld. Adapun residual Schoenfeld terdapat ada setiap individu yang mengalami event untuk setiap variabel prediktor dalam model cox proportional hazard.
Tahapan dari perhitungan Goodness of fit dengan residual Schoenfeld pada asumsi proportional hazard terdiri atas:
1. Setiap variabel prediktor model Cox Proportional Hazard dan setiap objek yang mengalami event akan dihitung nilai residual Schoenfeld nya.
2. Mengurutkan waktu survival dimulai dari individu yang mengalami event pertama kali, hal ini disebut juga variabel rank survival time.
3. Melakukan pengujian korelasi berdasarkan hasil residual Schoenfeld yang diperoleh pada langkah pertama dibandingkan dengan variabel yang dihasilkan variabel rank survival time yang diperoleh pada langkah kedua.
Rumus yang digunakan untuk menghitung Residual Schoenfeld dari variabel prediktor ke-p dan individu yang mengalami event pada waktu tertentu adalah sebagai berikut.

Selanjutnya untuk hipotesis yang digunakan pada pendekatan goodness of fit dengan residual Schoenfeld yaitu
H0: Tidak terdapat korelasi atau hubungan antara residual Schoenfeld dan rank waktu survival
H1: Terdapat korelasi atau hubungan antara residual Schoenfeld dan rank waktu survival
Adapun untuk statistik uji yang digunakan untuk pengujian adalah sebagai berikut.

Berdasarkan statistik uji, jika

Maka diambil kesimpulan tolak H0 artinya terdapat korelasi atau hubungan antara residual Schoenfeld dan rank waktu survival.
Namun perlu diingat bahwa untuk dapat dikatakan memenuhi asumsi proportional hazard, yaitu jika kesimpulannya adalah Gagal Tolak H0. Artinya, tidak terdapat korelasi atau hubungan antara residual Schoenfeld dan rank waktu survival.
Referensi
Demikian penjelasan terkait Analisis Survival Cox Proportional Hazard. Apabila masih ada yang dibingungkan bisa langsung saja ramaikan kolom komentar atau hubungi admin melalui tombol bantuan di kanan bawah. Stay tuned di website https://exsight.id/blog/ agar tidak ketinggalan artikel-artikel menarik lainnya.

