
Dalam statistika, terdapat beragam jenis korelasi, seperti yang telah dibahas pada artikel Exsight topik Penjelasan Mengenai Uji Korelasi. Melanjutkan pembahasan sebelumnya, untuk bahasan artikel kali ini kita akan fokus pada suatu jenis korelasi yang cukup populer dan umumnya digunakan dalam statistika nonparametrik yaitu Korelasi Kendall’s Tau.
Tidak hanya penjelasan secara teoritis, nantinya akan dijabarkan pula penerapan Korelasi Kendall’s Tau dalam suatu studi kasus menggunakan software SPSS. Yuk simak artikel ini dengan seksama yaa!
Definisi
Korelasi Kendall’s Tau meruapakan suatu jenis korelasi yang digunakan untuk melihat ada atau tidaknya hubungan antar 2 variabel pada skala data ordinal.
Terdapat asumsi yang harus dipenuhi pada korelasi Kendall’s Tau yaitu data merupakan pasangan hasil pengamatan (X,Y) yang diperoleh dari dua pengukuran pada unit penelitian yang sama (1 sumber yang sama). Contoh data yang berasal dari sumber yang sama adalah data berat dan tinggi badan siswa. Di mana kedua data tersebut sama-sama berasal dari sumber yang sama, yaitu 1 orang siswa pasti memiliki berat dan tinggi badan.
Tujuan
Pada dasarnya, korelasi Kendall’s Tau bertujuan untuk membandingkan pasangan-pasangan data dan menghitung proporsi pasangan yang memiliki hubungan yang sama atau berbeda dalam kedua variabel.
Rumus Perhitungan
Hipotesis pengujian korelasi Kendall’s Tau adalah sebagai berikut
\begin{matrix}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,H_{0}:\tau =0\left ( tidak\, ada\, korelasi\, antara\, variabel\, X\, dan\, Y \right )\\
H_{1}:\tau \neq 0\left ( ada\, korelasi\, antara\, variabel\, X\, dan\, Y \right )\\
\end{matrix}Statistik uji untuk pengujian korelasi Kendall’s Tau yaitu
\widehat{\tau }=\frac{P-Q}{\frac{1}{2}n\left ( n-1 \right )}Jika ukuran data sampel lebih dari 10 maka distribusi yang digunakan adalah distribusi normal, dimana statistik uji yang digunakan adalah sebagai berikut.
z=\frac{3\widehat{\tau }\sqrt{n\left ( n-1 \right )}}{\sqrt{2\left ( 2n+5 \right )}}Berdasarkan statistik uji pada persamaan di atas, maka untuk penentuan hipotesis dikatakan tolak jika:
\begin{matrix}
p-value<\alpha\, \, atau \\
\left \|tau \right |> \tau _{\frac{\alpha }{2},n}\, \, atau\\
\left \| z \right \|>z_{\frac{\alpha}{2}}
\end{matrix}Keterangan Simbol-Simbol pada Rumus:
\begin{matrix}
\tau =Koefisien\, korelasi\\
P=Jumlah\, Pasangan\, Data\, Berurutan\, Wajar\\
Q=Jumlah\, Pasangan\, Data\, Berurutan\, Terbalik\\
n=Jumlah\, Data\, Sampel\, Keseluruhan\\
z=Koefisien\, Korelasi\, ketika\, Data\, Lebih\, dari\, 10\\
\alpha =Taraf\, Signifikansi(alfa)\\
\end{matrix}Studi Kasus
Dalam studi kasus kali ini, kita akan menggunakan data sampel terkait Kedai Ayam Goreng di suatu daerah. Peneliti ingin meneliti apakah terdapat hubungan atau korelasi antara Harga Ayam Goreng (X) dan Kepuasan Pembeli (Y).

Pengumpulan data dilakukan dengan cara peneliti membagikan kuisioner kepada 40 pembeli di Kedai Ayam Goreng secara random. Adapun dataset dapat diakses disini. Rentang skor penilaian terkait jawaban responden yaitu 1 sampai 5 yaitu:
- 1= Sangat Tidak Puas
- 2=Tidak Puas
- 3=Cukup Puas
- 4=Puas
- 5=Sangat Puas
Tutorial SPSS Korelasi Kendall’s Tau
1.Buka software SPSS, kemudian entry data pada variable view dan data view.

Pada bagian data view berisi data-data dari masing-masing variabel, sedangkan untuk bagian variable view berisi pendefinisian dari masing-masing (khususnya terkait jenis data pada bagian measure).

2. Tahapan selanjutnya klik Analyze – klik Correlate – klik Bivariate

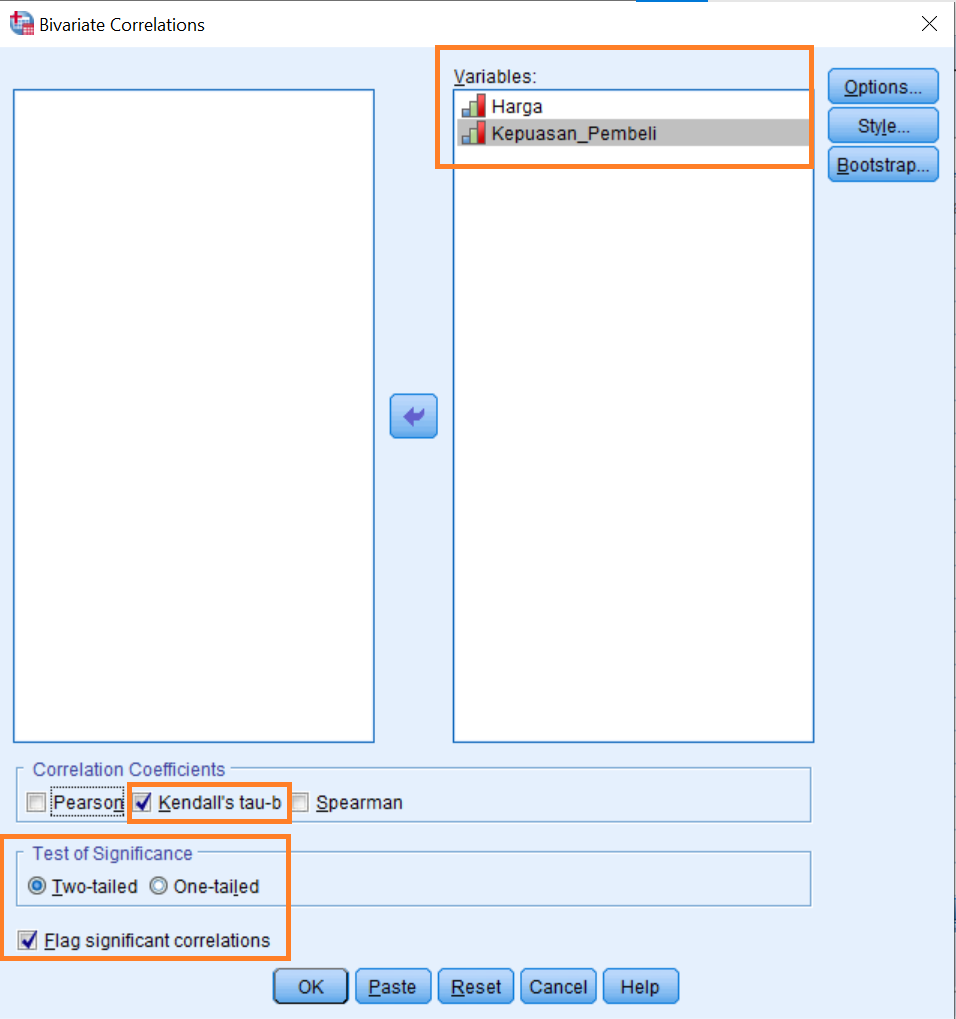
3. Selanjutnya akan muncul dialog box Bivariate Correlations, dimana pada bagian Variables kita masukkan semua variabel yaitu variabel Harga dan variabel Keputusan Pembeli. Lalu pada bagian Correlation Coefficients kita centang Kendall’s tau-b, pada bagian Test of Significance kita pilih Two-tailed dan Flag significant correlations.
Pembahasan Hasil Output SPSS
Hasil output SPSS adalah sebagai berikut. Interpretasi hasil dalam hal ini terdiri atas 3 bagian yaitu:
- Berdasarkan nilai signifikansi untuk melihat hubungan antar variabel
- Untuk melihat tingkat keeratan hubungan antar variabel
- Untuk melihat arah hubungan antar variabel .

1. Interpretasi berdasarkan nilai signifikansi untuk melihat adanya hubungan antar variabel
Dalam hal ini kita berfokus pada hasil output nilai signifikansi (p-value) atau Sig. (2-tailed) antara variabel Harga dan Kepuasan Pembeli, yaitu sebesar 0,001. Nilai Sig.(2-tailed) kemudian dibandingkan dengan nilai alfa dimana untuk alfa yaitu sebesar 0,01.
Dikarenakan nilai Sig.(2-tailed) bernilai lebih kecil dari alfa sehingga dapat disimpulkan terdapat korelasi antara variabel Harga dan Kepuasan Pembeli.
2. Interpretasi untuk melihat tingkat keeratan hubungan antar variabel
Sebelum itu, kita perlu mengetahui kriteria tingkat keeratan hubungan antar variabel berdasarkan nilai koefisien korelasi yaitu sebagai berikut:
- 0,00 sampai dengan 0,25 artinya hubungan sangat lemah
- 0,26 sampai dengan 0,50 artinya hubungan cukup
- 0,51 sampai dengan 0,75 artinya hubungan kuat
- 0,76 sampai dengan 0,99 artinya hubungan sangat kuat
- 1,00 artinya hubungan sempurna
Berdasarkan Gambar 4. dapat kita lihat, untuk nilai koefisien korelasi antar variabel Harga dan Kepuasan Pembeli yaitu sebesar 0,469. Artinya variabel Harga dan Kepuasan Pembeli memiliki hubungan yang bersifat cukup.
3. Interpretasi untuk melihat arah hubungan antar variabel
Arah hubungan antar variabel dapat dilihat berdasarkan nilai koefisien korelasi apakah bernilai positif atau negatif. Berdasarkan Gambar 4. diketahui bahwa besar koefisien korelasi sebesar 0,469 , dimana nilai ini poisitif. Sehingga dapat diartikan variabel Harga dan Kepuasan Pembeli memiliki hubungan yang positif atau searah.
Referensi
Nah sampai disini dulu penjelasan terkait Tutorial Korelasi Kendall’s Tau dengan SPSS. Apabila masih ada yang dibingungkan bisa langsung saja ramaikan kolom komentar atau hubungi admin melalui tombol bantuan di kanan bawah. Stay tuned di website https://exsight.id/blog/ agar tidak ketinggalan artikel-artikel menarik lainnya.

