Regresi non linear merupakan suatu metode analisis regresi untuk mendapatkan model non linear yang digunakan untuk mengetahui hubungan antar variabel terikat dan variabel bebas. Apa sih perbedaan dari regresi linear dengan regresi non linear? Jadi, perbedaannya adalah hubungan antara variabel bebas dan variabel terikat pada regresi linear mengikuti garis lurus, sedangkan pada regresi non linear bisa mengikuti pola eksponensial, kuadratik, kubik, logaritmik atau bentuk lainnya selain garis lurus.
Macam-macam Regresi Non Linear
- Parabola kuadratik:

Dengan menggunakan metode kuadrat terkecil, maka, a,b, dan c dapat dihitung dari sistem persamaan:

- Parabola kubik :

Untuk menentukan nilai a, b, c, dan d dapat digunakan dengan sistem persamaan berikut:

- Eksponen

Besar nilai a dan b ditentukan menggunakan persamaan:

- Geometrik

Besar nilai a dan b ditentukan menggunakan persamaan:

- Gompertz

- Logistik

Besar nilai a, b, dan c ditentukan menggunakan persamaan:

- Hiperbola

Jika Ybar tidak ada yang bernilai nol, maka a dan b adalah
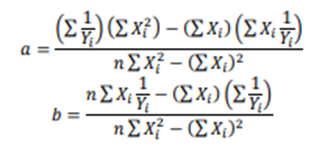
Kali ini kita akan membahas lebih lanju salah satu model yang termasuk dari Regresi Non Linear yaitu Model Regresi Logistik.
Model Regresi Logistik
Model regresi logistik merupakan regresi non linear dimana kurva hubungan antara variabel respon dan variabel prediktornya tidak berbentuk garis lurus. Regresi logistik digunakan untuk menggambarkan hubungan antara variabel respon dengan sekumpulan variabel prediktor, dimana variabel respon bersifat biner atau dikotomus. Variabel dikotomus adalah variabel yang hanya mempunyai dua kemungkinan nilai, misalnya sukses atau gagal. Model regresi logistik mengikuti distribusi bernoulli, dengan fungsi probabilitasnya adalah sebagai berikut (Haridanti, Adawiyah, & Ariadne, 2018):


Bentuk model regresi logistik adalah sebagai berikut:

Dengan,

Dalam regresi logistik memiliki 3 fungsi hubung yaitu sebagai berikut:
1. Regresi logit
Model regresi logit sering digunakan untuk kasus regresi logistik biner. Hal penting dalam fungsi logit yaitu inversnya harus memenuhi E(Y) antara 0 dan 1. Hal ini akan terpenuhi jika dengan menggunakan distribusi kumulatif atau CDF (Cumulative Distribution Function) sebagai invers fungsi hubung. Model regresi logit yaitu 𝑙𝑜𝑔𝑖𝑡[ 𝑃 𝑌 = 1] = 𝛽0 + 𝛽1𝑥1 + 𝛽2𝑥2 + ⋯ + 𝛽𝑝𝑥𝑝.
2. Regresi probit.
Invers dari CDF distribusi normal baku digunakan sebagai fungsi hubung. jika CDF dari distribusi normal baku dinotasikan dengan Φ (.), maka model dapat dituliskan sebagai 𝜋 = Φ (𝛽0 + 𝛽1𝑥1 + ⋯ + 𝛽𝑝𝑥𝑝). Umumnya probit (𝜋) sering digunakan dalam model sehingga model dapat ditulis sebagai probit(𝜋) = (𝛽0 + 𝛽1𝑥1 + ⋯ + 𝛽𝑝𝑥𝑝). Dengan catatan probit(𝜋) ekuivalen dengan Z_ 𝜋 yaitu kuantil normal baku pada peluang 𝜋.
3. Regresi log-log komplementer .
Invers dari distribusi nilai ekstrim yang digunakan untuk membentuk fungsi hubung. CDF-nya adalah 𝐹 (𝑥) = exp{ – exp [- 𝑥 – 𝜇]/𝜎]} untuk -∞ < 𝑥 < ∞ dan parameter -∞ < 𝜇 < ∞ dan 𝜎 > 0. Model regresi log-log komplementer dapat ditulis dengan 𝜋 = 1 – exp {- exp [𝛽0 + 𝛽1𝑥1 + ⋯ + 𝛽𝑝𝑥𝑝]} atau atau log [- log (1 – 𝜋) = 𝛽0 + 𝛽1𝑥1 + ⋯ + 𝛽𝑝𝑥𝑝 ].
Contoh Regresi Logistik
Gunakanlah data berikut ini dan lakukanlah analisis untuk membangun model yang dapat memprediksi apakah seorang pegawai dapat melaksanakan tugas (1) atau tidak(0) berdasarkan satu variabel bebas yaitu pengalaman yang dimiliki (bulan).
| No | Month | Task |
| 1 | 14 | 0 |
| 2 | 29 | 0 |
| 3 | 6 | 0 |
| 4 | 25 | 1 |
| 5 | 18 | 1 |
| 6 | 4 | 0 |
| 7 | 18 | 0 |
| 8 | 12 | 0 |
| 9 | 22 | 1 |
| 10 | 6 | 0 |
| 11 | 30 | 1 |
| 12 | 11 | 0 |
| 13 | 30 | 1 |
| 14 | 5 | 0 |
| 15 | 20 | 1 |
| 16 | 13 | 0 |
| 17 | 9 | 0 |
| 18 | 32 | 1 |
| 19 | 24 | 0 |
| 20 | 13 | 1 |
| 21 | 19 | 0 |
| 22 | 4 | 0 |
| 23 | 28 | 1 |
| 24 | 22 | 1 |
| 25 | 8 | 1 |
Penyelesaian
- Memanggil Data di Program R Studio
> sukses<-read.table(file="C:\\Users\\HP 14-BW099TU\\Documents\\data set\\programmingtask.txt", TRUE)
> str(sukses)
'data.frame': 25 obs. of 3 variables:
$ months: int 14 29 6 25 18 4 18 12 22 6 ...
$ task : int 0 0 0 1 1 0 0 0 1 0 ...
$ fit : num 0.31 0.835 0.11 0.727 0.462 ...- Membuat Model Regresi Probit
> model_probit<-glm(task~months,data=sukses,family=binomial(link='probit'))
> summary(model_probit)
Call:
glm(formula = task ~ months, family = binomial(link = "probit"),
data = sukses)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8959 -0.7579 -0.3907 0.8101 1.9691
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.83787 0.69012 -2.663 0.00774 **
months 0.09686 0.03565 2.717 0.00659 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 34.296 on 24 degrees of freedom
Residual deviance: 25.380 on 23 degrees of freedom
AIC: 29.38
Number of Fisher Scoring iterations: 4Persamaan model regresi Probit yaitu

- Model Regresi Logit
> model_logit<-glm(task~months,data=sukses,family=binomial(link='logit'))
> summary(model_logit)
Call:
glm(formula = task ~ months, family = binomial(link = "logit"),
data = sukses)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8992 -0.7509 -0.4140 0.7992 1.9624
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.05970 1.25935 -2.430 0.0151 *
months 0.16149 0.06498 2.485 0.0129 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 34.296 on 24 degrees of freedom
Residual deviance: 25.425 on 23 degrees of freedom
AIC: 29.425
Number of Fisher Scoring iterations: 4Persamaan model regresi logit:

- Model Regresi Complementary log-log
> model3<-glm(task~months,data=sukses,family=binomial(link='cloglog'))
> summary(model3)
Call:
glm(formula = task ~ months, family = binomial(link = "cloglog"),
data = sukses)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9294 -0.7545 -0.4850 0.8484 1.8914
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.58224 0.95432 -2.706 0.00681 **
months 0.11046 0.04202 2.629 0.00857 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 34.296 on 24 degrees of freedom
Residual deviance: 25.677 on 23 degrees of freedom
AIC: 29.677
Persamaan model regresi complementary log-log:

Penutup
Hai gimana guys?? Mudah banget kan cara mengerjakan analisis regresi logistik di R. Kamu tidak perlu repot-repot lagi unuk mencari persamaan analisis regresi dengan menggunakan cara manual. Kamu bisa mengerjakannya dengan R agar lebih cepat selesai karena tinggal tulis kodingnya saja nanti outputnya akan keluar. Eitss jangan lupa masih ada artikel selanjutnya yang akan membahas Part 2, tentang analisis berganda jadi tetap stay tune yaa. Jika masih ada yang kurang jelas, atau masih bingung bisa bertanya di kolom komentar atau menghubungi admin melalui tombol WA yaa. Terima kasih.
Daftar Pustaka
Kismiantini (2020). Analisis Respon Biner. Modul Kuliah. Yogyakarta: Universitas Negeri Yogyakarta.
Kusumawati, R. (2019). Regresi Logistik. Modul Kuliah. Yogyakarta: Universitas Negeri Yogyakarta.